Die Lösung zur binären Klassifikation mit dem XGboost-Paket fürs maschinelle Lernen

Im wirklichen Leben werden wir ziemlich oft mit der Aufgabenklasse konfrontiert, bei der das Objekt der Prognose eine nominale Variable mit zwei Abstufungen ist, und wir müssen das Ergebnis eines Ereignisses vorhersagen oder eine Entscheidung in binärer Form basierend auf einem Datenmodell treffen. Zum Beispiel ist dies der Fall, wenn wir die Situation auf dem Markt mit dem Ziel einschätzen, eine endgültige Entscheidung zu treffen, ob es sinnvoll ist, in ein bestimmtes Instrument zu investieren oder nicht, oder ob ein Schuldner beim Gläubiger seine Schulden begleicht, oder ob ein Mitarbeiter ein Unternehmen bald verlässt etc.

Im Allgemeinen wird die binäre Klassifikation herangezogen, um die Wahrscheinlichkeit des Eintretens eines bestimmten Ereignisses mithilfe der Analyse einer Reihe von Kriterien zu berechnen. Zu diesem Zweck wurde die sogenannte abhängige Variable eingeführt (das Ergebnis eines Ereignisses), die nur einen von zwei Werten annehmen kann (die auch Parametern, Prädiktoren oder Repressoren genannt werden können).

Ich möchte darauf hinweisen, dass es mehrere lineare Funktionen in “R” für die Lösung solcher Aufgaben wie “glm” im Standardpaket der Funktionen gibt, hier werden wir aber die erweiterte Variante der binären Klassifikation untersuchen, die im “XGboost”-Paket vorhanden ist. Dieses Modell, der häufige Gewinner bei Kaggle-Wettbewerben, basiert auf dem Aufbau von binären Entscheidungsbäumen und kann Multithreading unterstützen. Weitere Informationen zur Umsetzung der Modellfamilie “Gradient Boosting” finden Sie hier:

Gradient-Boosting-Maschinen, ein Tutorium (Englische Version)
Gradient boosting (Wikipedia, englische Version)

Lassen Sie uns nun uns einen Test-Datensatz („train“) vornehmen und ein Modell bauen, um die Anzahl der bei einem Flugzeugabsturz überlebten Passagiere vorherzusagen:

    data(agaricus.train, package='xgboost')
    data(agaricus.test, package='xgboost')
    train <- agaricus.train
    test <- agaricus.test

Wenn die Matrix nach der Transformation eine Menge Nullen enthält, dann sollte solch ein Datenarray vorerst in eine dünnbesetzte Matrix transformiert werden — so werden die Daten viel weniger Platz einnehmen, folglich wird die für die Datenverarbeitung erforderliche Zeit erheblich reduziert. An diesem Punkt wird sich die ‘Matrix’-Bibliothek als nützlich erweisen, ihre letzte derzeit verfügbare Version 1.2-6 enthält eine Reihe Funktionen für die Transformation zu einer dgCMatrix mit Spalten. In den Fällen, in denen nach all den Transformationen, schon die dünnbesetzte Matrix nicht in den Direktzugriffsspeicher rein passt, wird ein spezielles Programm “Vowpal Wabbit” genutzt. Es ist ein externes Programm, das die Datensätze jeglicher Größen verarbeiten kann, indem sie aus vielen Dateien oder Datenbanken herausgelesen werden. “Vowpal Wabbit” ist eine optimierte Plattform fürs parallele maschinelle Lernen, die für die verteilte Verarbeitung von “Yahoo!” entwickelt wurde. Sie können darüber im Detail nachlesen, wenn Sie dem Link folgen:

Vowpal Wabbit (Wikipedia, englische Version)

Durch die Verwendung von dünnbesetzten Matrizes können wir ein Modell bauen, indem wir die Textvariablen mit ihrer vorläufigen Transformation nutzen.
Somit sollten wir, um eine Matrix von Prädiktoren zu bauen, zuerst die erforderlichen Bibliotheken herunterladen:

    library(xgboost)
    library(Matrix)
    library(DiagrammeR)

Während der Umwandlung in die Matrix werden alle kategorischen Variablen übertragen, also eine Funktion mit einem Standard-Booster wird deren Werte in ein Modell transportieren. Das Erste, was zu tun wäre, ist, aus dem Datensatz die Variablen mit den einzigartigen Werten, wie “Passagier-ID“, “Name“ und” Ticketnummer” zu entfernen. Dann machen wir das Gleiche mit dem Textdatensatz, der für die Berechnung der Ergebnisprognosen verwendet wird. Zur Veranschaulichung habe ich die Daten aus den lokalen Dateien geladen, die ich in den entsprechenden Kaggle-Datensatz heruntergeladen habe. Für das Modell brauchen wir die folgenden Tabellenspalten:

    input.train <- train[, c(3,5,6,7,8,10,11,12)]
    input.test <-  test[, c(2,4,5,6,7,9,10,11)]

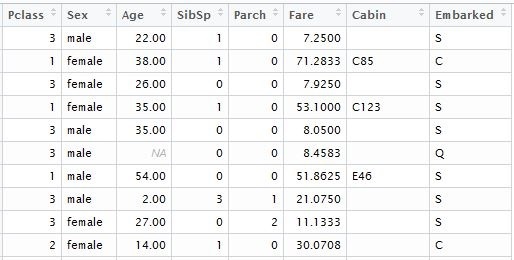
Wir bilden getrennt den Vektor der bekannten Ergebnisse für das Modell:

    train.lable <- train$Survived

Nun ist es notwendig, die Datentransformation für die statistisch signifikanten Variablen auszuführen, die berücksichtigt werden sollen. Lassen Sie uns folgende Transformationen ausüben:

Wir ersetzen die Variablen, die kategorische Daten mit numerischen Werten enthalten. Zugleich sollte man berücksichtigen, dass die geordneten Kategorien, wie “gut”, “normal”, “schlecht” durch 0,1,2 ersetzt werden können. Die Daten mit der relativ geringen Selektivität, wie “Geschlecht” oder “Land”, können als faktorielle Daten unverändert bleiben. Nach der Transformation zur Matrix werden sie in eine entsprechende Anzahl an Spalten mit Nullen und Einsen übertragen. Bei numerischen Variablen ist es notwendig, alle nicht zugewiesenen und fehlenden Werte zu verarbeiten. Es gibt mindestens 3 Varianten dazu: Sie können mit 1,0 ersetzt werden oder, was eine hinnehmbarere Variante wäre, sie können durch den durchschnittlichen Wert der Spalte für diese Variable ersetzt werden.

Bei der Nutzung des “XGboost”-Pakets mit einem Standard-Booster (gbtree) kann die Variablenskalierung weggelassen werden, im Gegensatz zu den anderen linearen Methoden, wie “glm” oder “xgboost” mit einem linearen Booster (gblinear).

Die wichtigsten Informationen über das Paket finden Sie über die folgenden Links:

xgboost (GitHub, englische Version)
Paket ‘xgboost’ (PDF, englische Version)

Zurück zu unserem Code: Als Ergebnis haben wir eine Tabelle im folgenden Format bekommen:

Danach müssen wir alle fehlenden Angaben durch das arithmetische Mittel aus der Prädiktorenspalte ersetzen:

    if (class;(inp.column) %in %c('numeric', 'integer')) {
        inp.table[is.na(inp.column), i] <- mean(inp.column, na.rm=TRUE)

Nach der Vorverarbeitung brauchen wir die Transformation zur “dgCMatrix”:

sparse.model.matrix(~., inp.table)

Es ist durchaus sinnvoll, eine separate Funktion zur Vorverarbeitung von Prädiktoren und zur Transformation zum sparse.model.matrix-Format zu erstellen, die Version mit dem Zyklus “for” ist z.B. untenstehend angeführt. Zur Leistungsoptimierung können Sie die Auswirkung mithilfe der Funktion “apply” vektorisieren.

    spr.matrix.conversion <- function(inp.table) {
        for (i in 1:ncol(inp.table)) {
            inp.column <- inp.table [ ,i]
            if (class(inp.column) ==         'character') {
                inp.table [is.na(inp.column), i] <- 'NA'
                inp.table [, i] <- as.factor(inp.table [, i])
            }
            else
                if (class(inp.column) %in% c('numeric', 'integer')) {
                    inp.table [is.na(inp.column), i] <- mean(inp.column, na.rm=TRUE)
                }
        }
    return(sparse.model.matrix(~.,inp.table))
    }

Anschließend werden wir unsere Funktion nutzen und die Fakten- und Texttabellen in dünnbesetzte Matrizen verwandeln:

    sparse.train <- preprocess(train)
    sparse.test <- preprocess(test)

Um dieses Modell zu bauen, brauchen wir zwei Datensätze: Die Datenmatrix, die wir gerade eben erstellt haben, und
einen Vektor der tatsächlichen Ergebnisse mit einem binären Wert (0,1).

Die “Xgboost”-Funktion ist die benutzerfreundlichste. In “XGBoost” ist ein Standard-Booster implementiert, der auf binären Entscheidungsbäumen basiert.

Um “XGboost” zu verwenden, müssen wir eine der drei Parameterarten auswählen: Allgemeine Parameter, Booster-Parameter und Zweck-Parameter:

• Allgemeine Parameter – wir definieren, welcher Booster verwendet wird, entweder der lineare oder der Standard-Booster.
• Die Auswahl anderer Parameter hängt davon ab, welcher Booster in dem ersten Schritt ausgewählt wurde:
• Parameter der Lernaufgabe – wir definieren den Zweck und das Szenario des Lernens
• Parameter der Befehlszeile – sie werden verwendet, um den Modus einer Befehlszeile mithilfe von “xgboost” zu bestimmen.

Die allgemeine Form der “xgboost”-Funktion, die wir verwenden, ist wie folgt:

    xgboost(data = NULL, label = NULL, missing = NULL, params = list(), nrounds, verbose = 1, print.every.n = 1L, early.stop.round = NULL, maximize = NULL, ...)

“data” – Matrixformatdaten (“matrix”, “dgCMatrix”, lokale Datendatei oder “xgb.DMatrix”)

“label” – Vektor der abhängigen Variablen. Wenn ein bestimmtes Feld Teil einer Quelltabelle von Parametern war, dann sollte es vor der Verarbeitung und Transformation zur Matrix ausgeschlossen werden, um die Transitivität der Verbindungen zu vermeiden.

“nrounds” – Anzahl der Entscheidungsbäume im endgültigen Modell.

“objective” – Durch diesen Parameter übertragen wir die Aufgaben und das Lernziel eines Modells.

“reg:logistic” – Logistische Regression mit einem binären Wert der Prognose.

Für diesen Parameter können wir einen bestimmten Grenzwert von 0 bis 1 setzen. Standardmäßig ist dieser Wert auf 0,5 eingestellt.

Über die Parametrisierung eines Modells können Sie unter diesem Link nachlesen:

XGBoost-Parameter (Englische Version)

Nun lassen Sie uns zum Erstellen und Einsatz des “XGBoost”-Modells übergehen:

    set.seed(1)
    xgb.model <- xgboost(data=sparse.train, label=train$Survived, nrounds=100, objective='reg:logistic')

Falls gewünscht, ist es möglich, die Struktur der Bäume mithilfe der Funktion xgb.model.dt.tree (model = xgb) abzuleiten. Danach sollten wir die Standardfunktion “predict” verwenden, um den Prognosevektor zu bilden:

    prediction <- predict(xgb.model, sparse.test)

Und schließlich müssen wir die Daten in einem lesbaren Format abspeichern:

    solution <- data.frame(prediction = round(prediction, digits = 0), test)
    write.csv(solution, 'solution.csv', row.names=FALSE, quote=FALSE)

Wenn wir den Vektor der prognostizierten Ergebnisse hinzufügen, erhalten wir die folgende Tabelle:

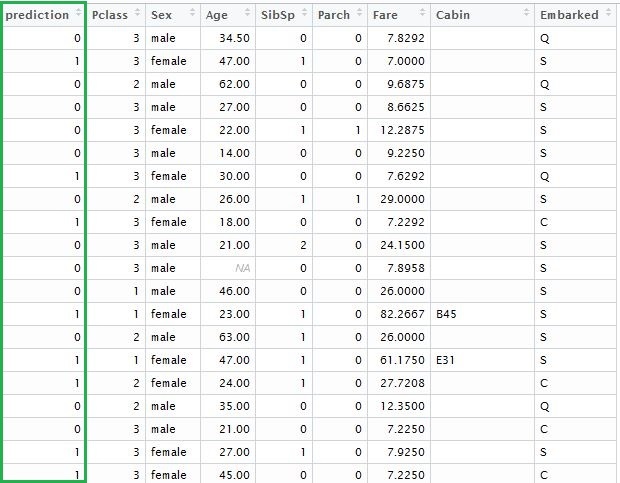
Gehen wir kurz zurück und überprüfen das Modell, das wir gerade eben erstellt haben. Wir können die Funktionen “xgb.model.dt.tree” und “xgb.plot.tree” verwenden, um die Entscheidungsbäume anzeigen zu lassen. Z.B. wird uns die letztere Funktion eine Liste der ausgewählten Bäume mit dem Koeffizienten der Modellanpassung generieren:

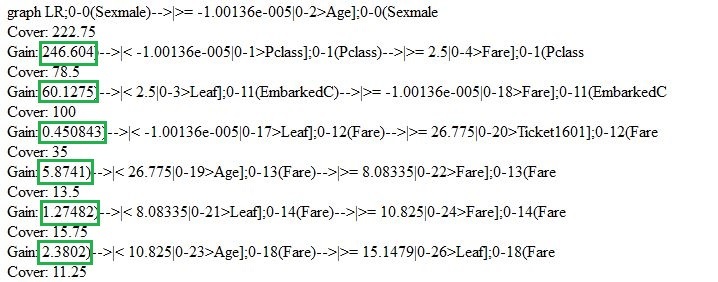
Mithilfe der Function xgb.plot.tree können wir auch die Grafik-Darstellung der Bäume sehen. Es sollte jedoch darauf hingewiesen werden, dass sie in der aktuellen Version nicht auf die beste Art und Weise umgesetzt wurde und daher weniger brauchbar ist. Deswegen musste ich, um dies zu verdeutlichen, den grundlegenden Entscheidungsbaum manuell aufgrund des Train-Standarddatenmodells reproduzieren.

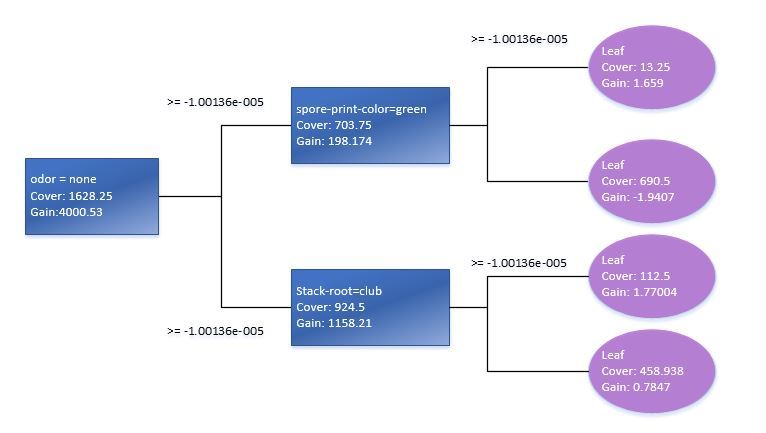
Die Prüfung der statistischen Signifikanz der Variablen in einem Modell wird uns aufzeigen, wie die Matrix der Prädiktoren für das XGB-Modelllernen zu optimieren ist. Am besten ist dafür die Funktion xgb.plot.importance zu nutzen, in die wir die aggregierte Tabelle der Parameterbedeutung übertragen.

    importance_frame <- xgb.importance(sparse.train@Dimnames[[2]],  model = xgb)
    xgb.plot.importance(importance_frame)

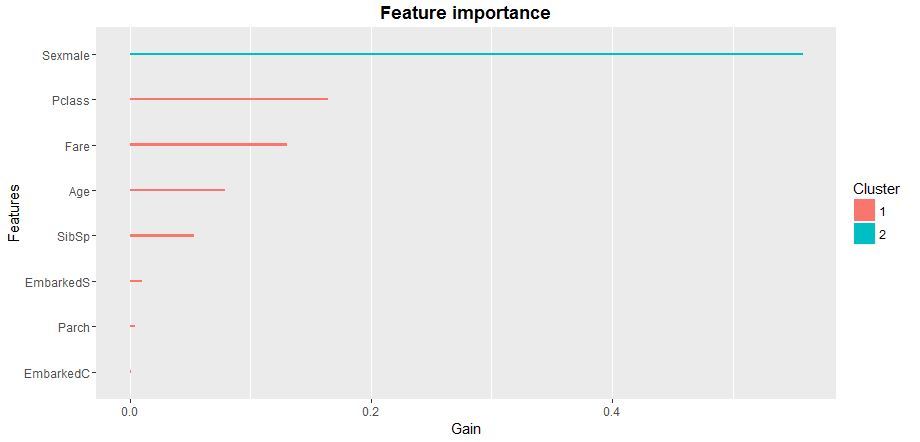
Zusammenfassend lässt sich sagen, dass wir eine der möglichen Implementierungen der logistischen Regression überprüft haben, die auf dem Paket der “xgboost”-Funktion mit einem Standard-Booster basiert. Ich empfehle das “XGboost”-Paket, weil es die mit Abstand am weitesten fortgeschrittene Gruppe der Modelle fürs maschinelle Lernen repräsentiert. Derzeit sind die Vorhersagemodelle auf der Basis der “XGboost”-Logik im Bereich der Finanz- und Marktprognosen, im Marketing und in vielen anderen Bereichen der angewandten Analytik und des maschinellen Lernens weit verbreitet.